Heuer ist die Kartoffelernte sehr dürftig ausgefallen. Das veranlasst mich, einen Beitrag zu schreiben, den ich schon seit langer Zeit auf meiner Ideenliste habe.
Eingefallen war mir das mal vor einiger Zeit, als ich mit Kartoffelschälen beschäftigt war. Die Kartoffeln waren sehr klein, was bedeutet, dass ich für die gleiche Menge Kartoffeln deutlich länger beschäftigt war, als damals, als ich schöne große Kartoffeln hatte.
Warum ist das so? Zunächst einmal ist da ein Offset, weil man jede einzelne Kartoffel in die Hand nehmen muss und sie zurechtdrehen. Kein Wunder, dass man bei vielen kleinen Kartoffeln länger braucht als bei wenigen großen – auch wenn die Gesamtmasse gleich ist.
Bei kleinen Kartoffeln muss man trotzdem den Schäler fast genauso oft ansetzen, kann aber nur kürzere Schalenstücke in einem Zug entfernen.
Dazu kommt, dass man bei kleinen Kartoffeln mehr Abfall hat als bei großen.
Und das werde ich im folgenden vorrechnen.
Gegen wir davon aus, dass sich die Kartoffeln zusammensetzen aus jeweils gleichgroßen Kugeln.
Das Volumen einer Kartoffel mit dem Radius r ist V_K = 4/3 * pi * r^3.
Für nicht allzu kleine Kartoffeln ist das Volumen des geschälten Abfalls näherungsweise gleich ihrer Oberfläche mal der Schichtdicke d: V_S = 4 * pi * r^2 * d.
Vergleicht man nun den Schalenanteil mit dem Gesamtvolumen, so erhält man: V_S / V_K = 3 * d / r.
Die Abfallmenge ist also indirekt proportional zum Radius der Kartoffel. Je dünner die abschälte Schale ist, desto weniger Abfall. Das ist leicht nachvollziehbar und in etwa linear (für hinreichend große Kartoffeln).
Für eine Kartoffelmenge der Masse m benötigt man n = 3 * m / (4 * pi * rho * r^3) Kartoffeln, wobei wir davon ausgehen, dass die Dichte rho konstant sei.
Es ist also nicht überraschend, dass kleinere Kartoffeln merklich mehr Arbeit machen, denn die Abhängigkeit ist kubisch.
Auch wenn die Rechnung exakt nur für kugelförmige Kartoffeln gilt, ist sie auch plausibel für anders geformte Kartoffeln. (Wobei wir selbstverständlich im Hinterkopf behalten, dass eine Kugeloberfläche ja eine Minimalfläche ist. D.h., dass bei anderen Formen der Verschnittanteil eher ungünstiger wird.)
Gehen wir von einer Schichtdicke von 1 Millimeter aus, so hat eine mickrige Kartoffel mit 3 Zentimeter Durchmesser einen Verschnitt von zwanzig Prozent, während eine Riesenkartoffel mit 12 Zentimeter Durchmesser nur fünf Prozent Abfall generiert.
Dabei gehen wir davon aus, dass die Kartoffeln ansonsten einwandfrei sind – ohne Augen oder schlechte Stellen. Es funktioniert auch nur, solange sie halbwegs frisch sind, so dass die Schale glatt und prall auf ihnen liegt. Ältere Kartoffeln haben Feuchtigkeit verloren, so dass sie schrumpelig werden, und man sie nur noch unter Schwierigkeiten im Rohzustand schälen kann. Dann hilft nur noch, sie erst zu kochen und danach zu pellen.
(Und ja, es ich mir bekannt, dass man die Schale auch mitessen kann, wenn man die Kartoffeln vor dem Kochen gründlich mit einer Bürste reinigt. Ob das Abbürsten jetzt unbedingt weniger Arbeit macht, lassen wir mal dahingestellt. Für manche Gerichte mag ich aber einfach keine Schale dran haben.)

Gut, dass wir in einem dreidimensionalen Raum leben. In hochdimensionalen Räumen befindet sich der größte Teil der Kartoffel in der Nähe der Schale und geht beim Schälen als Verschnitt verloren.
LikeGefällt 1 Person
Vielleicht würde aber die Topologie einer solchen Hyperkartoffel es erlauben, sie von innenheraus zu verzehren, ohne sie schälen zu müssen, bzw. die Schale wie einen Kern zu entfernen.
LikeGefällt 1 Person
Ich steh‘ total auf Hyperkartoffeln!
LikeGefällt 1 Person
Diese Überlegung stelle ich regelmäßig beim Kauf von Kartoffeln an. Die Proportionalität des Verschnitts zum Reziproken des Volumens der Kartoffeln ist immer da, nur der Vorfaktor variiert – als „Formfaktor“ 😉 Zumindest in einem nur geringfügig erweiterten Model und unter der Annahme, dass große Kartoffeln nicht sehr viel anders geformt sind als kleine und der Voraussetzung, dass die Abweichung von der Kugelform in ihren lokalen Krümmungsradien klein gegenüber der Schälen-Verschnitt-Dicken sind.
LikeGefällt 1 Person
Ja, so ähnlich lassen sich die Überlegungen ebenfalls auf anderes Obst und Gemüse, das man schälen möchte, ausdehnen.
LikeGefällt 1 Person
Warum müssen die Kartoffeln vor dem Kochen gründlich abgebürstet werden, wenn man die Schale mitessen will? Ich finde, einfach Waschen mit den Händen, so dass die Reste von Erde usw. weg sind, reicht aus. Alles, was dann noch an Keimen usw. vorhanden ist, wird doch durch die Hitze des kochenden Wassers sowieso abgetötet?
LikeGefällt 1 Person
OK, „müssen“ war übertrieben.
Aber ich habe durchaus schon Kartoffeln erlebt, an denen Erde stark verkrustet geklebt war. Da erleichtert bürsten das Entfernen.
LikeLike
Wasser hat immer ausgereicht – manchmal muss man halt etwas mehr mit den Fingern schrubben, aber eine Bürste hab ich mir noch nie gewünscht. Ich koche aber auch nur sehr selten Kartoffeln 😉
LikeLike
Kartoffelschälen war schon als Kind, noch mit einem kleinen Schälmesser, eine schöne Art zu entspannen und die Gedanken dahinfließen zu lassen.
Wobei ich meist versucht habe, eine Kartoffelschale, ohne Unterbrechung, zu bekommen und dabei so wenig wie möglich von der Kartoffel an der Schale dran zu lassen.
LikeGefällt 1 Person
Wenn man keinen Zeitdruck hat, hat Kartoffelschälen schon etwas meditatives.
Das mit den langen Schalenschlangen mache ich manchmal bei Äpfeln. Aber da habe ich auch nur ein oder zwei zu schälen, während es bei Kartoffeln meist größere Mengen sind.
LikeGefällt 1 Person
Es fehlt nun zur Vollständigkeit der Nudelindex oder zumindest der Soßénaufnahmeindex von Nudeln, der so wichtig bei der Gulaschsoße ist.
LikeGefällt 1 Person
Das Fliegende Spaghettimonster möge mit dir sein!
RAmen.
LikeGefällt 2 Personen
Genau !
Lecker Spaghetti mit Bolo ! Mälzer-Style.
LikeLike
Wie gut, dass ich keine Salzkartoffeln mag … 😉
LikeLike
Was ist mit Pommes Frites? Oder Kartoffelpüree?
Dafür müssen die Kartoffeln ja auch vorher geschält werden.
LikeLike
@ Anne
Bist Du sicher, dass Du ne Frau bist? 😀
Solche Gedankenexperimente stellen doch sonst nur Männer an.
Zur Vereinfachung Deiner Rechnung (hat mich mal ne Kommilitonin(!) während des Studium drauf hingewiesen) gilt: bei linear steigendem Durchmesser steigt die Oberfläche mit der zweiten, das Volumen mit der dritten Potenz. Da die Schalendicke nicht mitwächst, also unabhängig von der Kartoffelgröße ist, kann man annähernd sagen, dass sie ebenfalls mit der zweiten Potenz steigt.
Also -> große Kartoffeln haben ein günstigeres Speise/Abfallverhältnis 😉
Ich hatte vor langer Zeit mal eine ziemlich leichte Aufgabe bei AE eingestellt, die total unserem mathematischen Gefühl widerspricht – zumindest meinem. Ist auch immer wieder n nettes Spiel unter Kollegen.
Vielleicht hat ja jemand Lust, die Aufgabe aus- und nachzurechnen 🙂
Also: wir nehmen an, die Erde ist eine perfekte Kugel mit einem Umfang von 40.000 km.
Um diese Erde legen wir nun bündig einen Metallring entlang des Äquators. Dieser Ring hat die Länge von besagten 40.000 km.
Jetzt trennen wir den Metallring an einer Stelle auf und verlängern ihn um 1 m.
Nehmen wir an, dieser Ring würde nun kreisrund über der Oberfläche der Erde schweben.
Frage: wie weit ist der Ring von der Erdoberfläche entfernt?
1. 16 u (Atomgröße)
2. 16 µm
3. 16 mm
4. 16 cm
5. 1,6 m
Also, ich war vom Ergebnis mehr als überrascht und hatte es deshalb mehrmals durchgerechnet. Aber es stimmte 😀 😀
LikeLike
Lach. Die kenne ich noch aus’m Mathebuch.
LikeLike
Sofern man rein biologische Kriterien anwendet, bin ich mir da schon sehr sicher. Bei genderistischer Betrachtung nicht mehr ganz so sehr.
Ja, der Abfallanteil steigt allgemein (näherungsweise) linear. Bei Kugeln ist der Formfaktor (wie vorgerechnet 3), bei Würfeln wäre er 6.
Antwort 4: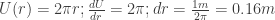
Als gelegentliche Kunststrickerin ist mir das geläufig (2*pi zusätzliche Maschen pro Runde, unabhängig vom Radius, um eine kreisförmige Decke zu stricken).
LikeLike
Das „unabhängig vom Radius“ ist das Entscheidende, das es schwer macht, das Ergebnis intuitiv zu erfassen.
Selbst wenn man den beschriebenen Ring ums ganze (kugelförmig angenommene) Universum spannen würde, würde seine Verlängerung um 1 m zu einem Abstand von 16 cm führen.
Am einfachsten lässt sich die Variante mit einem Atom als Kugel berechnen, bei der man der Einfachheit halber den Kugeldurchmesser auf Null setzt.
Dass man das sogar bei der Kunststrickerei lernt, haut mich nun allerdings echt nochmal um 😀
LikeGefällt 1 Person
Och, beim Stricken lernt man so einiges.
Beispielsweise auch, dass Rechte und Linke exakt gleich aussehen, wenn man sie von der jeweils anderen Seite betrachtet.
LikeLike
Politik beim Stricken? 😉
(beim hochhäkeln verlorener Maschen ist das aber praktisch – ich bekomme das hochhäkeln linker Maschen nicht so gut hin – also einfach umdrehen :-))
LikeLike
Hochhäkeln kann ich auch nur die rechten Maschen. Ein topologisches Problem.
LikeLike
Pingback: Twitteralien //2146 | breakpoint
Pingback: Freizeit mit Kindern //2201 | breakpoint
Pingback: Kartoffeln und Würstchen //2237 | breakpoint
Pingback: Die größten Kartoffeln //2977 | breakpoint
Pingback: Full House am Oster?o{n}tag //3029 | breakpoint